簡介 - Instance Segmentation by Jointly Optimizing Spatial Embeddings and Clustering Bandwidth
Davy Neven, Bert De Brabandere, Marc Proesmans, Luc Van Gool. Instance Segmentation by Jointly Optimizing Spatial Embeddings and Clustering Bandwidth. In CVPR’19.
CVPR 2019 paper
Paper link: https://arxiv.org/abs/1906.11109
Github(2019. Jul. 27 還沒釋出,請關注此網址): https://github.com/davyneven/SpatialEmbeddings
簡介
此論文針對實例語意分割(Instance Segmentation)的任務進行研究,
現存的 Instance Segmentation 若要有不錯的準確度都是使用 Proposal-based(Object detection 的概念) 的方法,
就是透過 Region proposal 先框出物體,
而這方法往往速度慢以及能處理的圖片解析度無法很高,
不適合運用在自動駕駛的情況下 - Real time,
此論文提出 Proposal-free 來改良上述問題,
雖然此框架準確度仍然無法達到 Proposal-based 方法的水平,
但提供了一個不錯的思路來解決速度以及高解析度的問題,
其概念為同個物體所預測的中心點越靠近越好,
當預測出的中心點(Spatial embedding)的越準確,
我們就能很輕易的提取出各個物件。

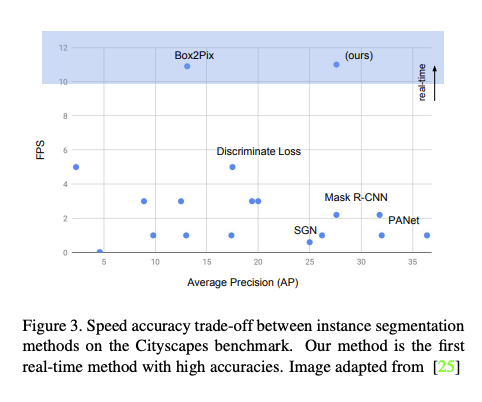
此方法評估在 Cityscapes 的資料集,
不僅速度提升、準確度還略高於 Mask-RCNN。
概念
Instance segmentation 首先要找到物體的中心點 C,
然後要找出目前該 Pixel 是對應到哪個中心點,
而通常一個照片會有多個物體 S = {S_0…S_K},代表著會有 K 個中心點 - C。
最簡單的做法是將該物體的所有座標平均當作中心點。
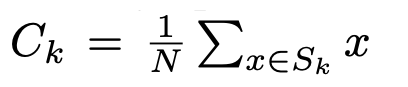
那我們模型要做的事情是學習目前這個點和中心點 C 的差距(Offset)為多少,
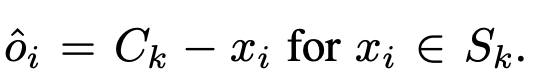
訓練方式就是透過 Regression 的方式。
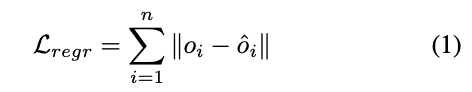
而我們可以把式子改一下,
目前的座標加上預測出的 Offset = e(Spatial embedding),
ei,j 預測自身物體的中心點座標。
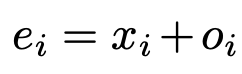
因此我們整理一下上方的概念,
如果要處理好 Instance segmentation 的任務,
有兩件事很關鍵
- 要得到好的中心點 C = {C_0, C_1, …, C_k}
- 每個 Pixel 預測出的 Offset 要靠近中心點。
針對第一個點,
之前的方式都是使用 Density-based clustering 的方式來提取出中心點 C = {C_0, C_1, …, C_k}。
而針對第二點以往的訓練方式是採用 Regression-based,
讓預測出來的 e(Spatial embedding) 越靠近中心點越好。
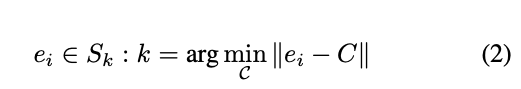
方法
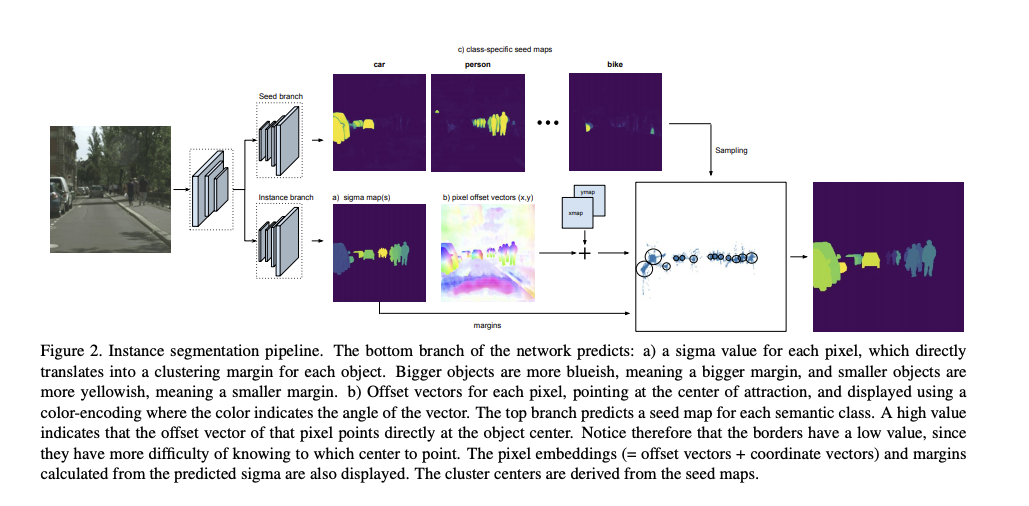
主要架構為兩部分
- Seed branch (在 Inference 的時候找出中心點)
- Instance branch (學習該 Pixel 的中心點在哪)
會先從 Instance branch 開始作介紹!!
在概念的部分有講到要針對中心點的學習,
此論文放寬限制讓他採用 Hinge loss 的方式,
如果他中心點已經學得夠好的話,就不會給 Loss。
舉例來說可能我們會覺得預測中心點的座標在 +- 2 之間都已經算學得很好了,
這時候我們的 Margin - δ 就會設定在 2。
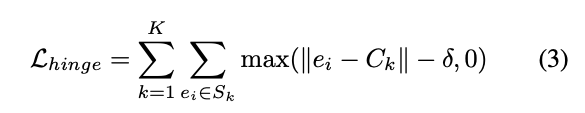
那在 Inference 的時候,
我們預期提取出的中心點 C 是準的,
Clustering 時就可以用比較簡單的方式,
各個 Pixel 所預測出的 e(預測的中心點)相近的視為是同一個物體。
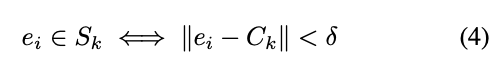
但這邊有個缺點,這個 Margin 要怎麼設定??
如果給太小的話,我們雖然確保小物體之間可以被正確的分出,
但是他會損害大物體的準確率,
因為我們會認為大物體的 Margin 可以給大一點設定的較為寬鬆。
基於上面的想法,
作者認為我們模型應該去學習各個物體的要給什麼 Margin,
如果物體大 Margin 可以給大一點,
但是物體小的時候就要給小一點,
透過 Margin 的概念,
我們的預測的 e 可以不用準確的預測到中心的位置。
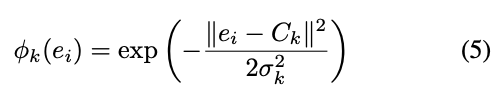
當輸出的分數高的時候,
代表靠中心點越近也代表我們所學出來的 e 是可信的。
得到 Sigma 的方式則是模型預測的,
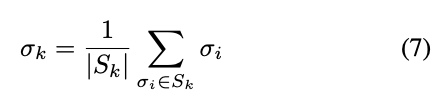
那 Margin 的概念可以使用 Guassion 的方式去定義,
定義 Margin 為:
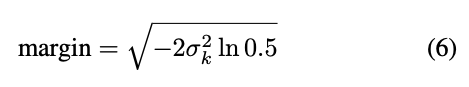
Elliptical Margin
只是說使用一個值當作 Sigma,
它只會產生出圓形的 Margin,
不如分別預測出 x, y 的 Sigma,
讓他可以產生出橢圓形的 Margin
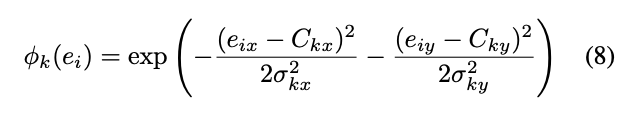
Learnable Center of Attraction
比起使用中心點 C 去做訓練,
使用預測出來的點 e 當作 C 去做訓練反而效果更好,
摁。。。這部分想看程式碼,但目前還沒有。
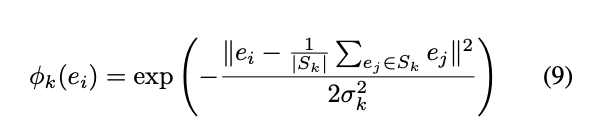
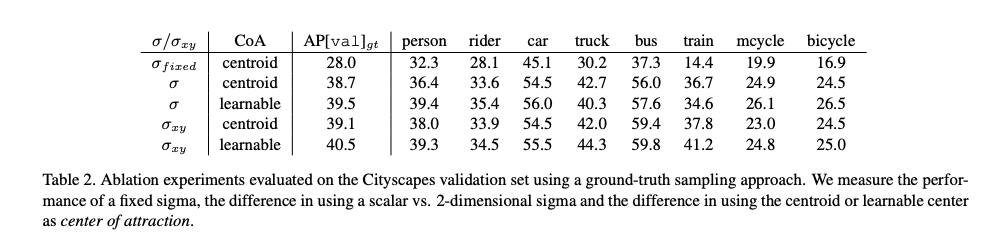
來先看看 Ablation study 的成效
Seed map
在 Inference 的時候我們會希望知道每個物件的中心點,
而這邊我們可以依賴 eq5 所預測出的分數,
當這個分數高的時候,我們會知道這個 Pixel 所預測出的 Embedding - 中心點是準的,
訓練方式就是使用 Regression 的方式,
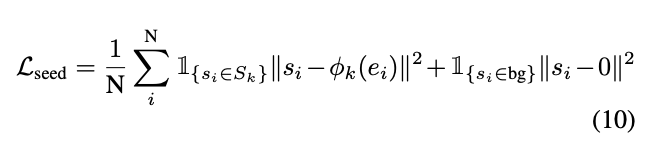
那基本上就是從這些分數高的隨便挑一個的 Embedding 當作中心點。
Post-processing
透過上面 Seed map 的部分,
我們知道可以從分數高的 Embedding 當作中心點,
在 Inference 的時候,
要將各個 Pixel 歸類到各個物體,
而判斷的標準就是那個 Pixel 的機率 > 0.5 為同一個物體,反之為背景。
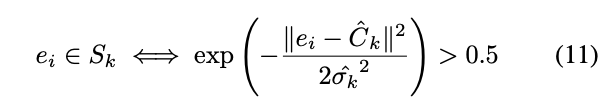
而為了確保每個 Pixel 的 Sigma 都差不多,
給出 Smooth loss function 來限制這個值。
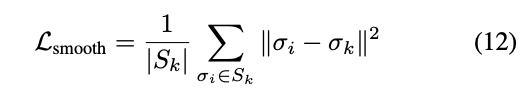
整體訓練細節
這部分好多,有興趣的去看論文,我提幾個就好。
話說我沒看到整體的 Total loss,
ERFNet 當作 Base-network,
在模型的 Instance branch 中會預測出 Sigma(1 或 2 個值-(x, y)) + 座標(x, y) 代表依據設定不同會預測出 3 或 4個值。
Loss function 為 Lovasz-hinge loss 而非以往的 Cross-entropy loss,
好處是他是考量每個物件的 iou 去做訓練。((這部分我沒去認真看,有興趣的自己去看那篇論文。
對於 Sigma 以及 Offset 並不是用 Supervised 的方式去做訓練,而是藉由最大化 iou 來 Joint 的訓練這兩個參數。
成果
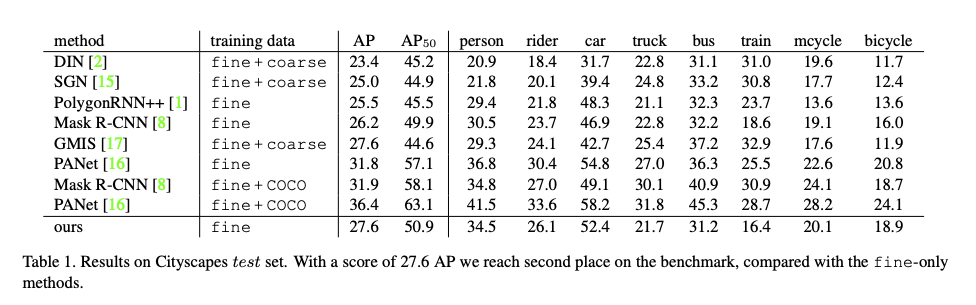
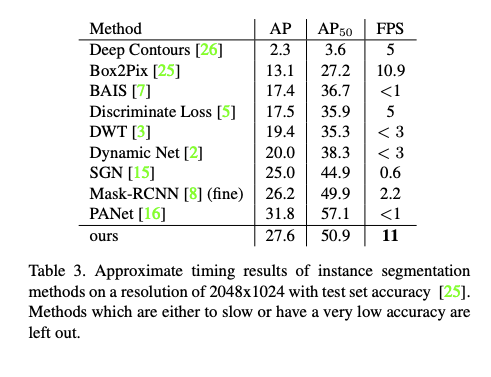

參考資料:
Instance Segmentation by Jointly Optimizing Spatial Embeddings and Clustering Bandwidth